MONOPOLY, MARGINAL ANALYSIS: A monopoly produces the profit-maximizing quantity of output that equates marginal revenue and marginal cost. This marginal approach is one of three methods that used to determine the profit-maximizing quantity of output. The other two methods involve the direct analysis of economic profit or a comparison of total revenue and total cost. Monopoly is a market in which a single firm is the only supplier of the good. Anyone seeking to buy the good must buy from the monopoly seller. This single-seller status gives monopoly extensive market control--a price maker that faces a negatively-sloped demand curve. With this negatively-sloped demand curve, marginal revenue is less than average revenue and price.Comparable to any profit-maximizing firm, a monopoly produces the quantity of output in the short run that generates the maximum difference between total revenue and total cost, which is economic profit. This profit maximizing level of production is also achieved by the equality between marginal revenue and marginal cost. At this production level, the firm cannot increase profit by changing the level of production. The analysis of marginal revenue and marginal cost can be achieved through a table of numbers or with marginal revenue and marginal cost curves. Working the NumbersA monopoly is presumed to produce the quantity of output that maximizes economic profit--the difference between total revenue and total cost. This decision can be analyzed using the exhibit below. This table presents revenue and cost information for Feet-First Pharmaceutical, a hypothetical example of a monopoly, for the production and sale of Amblathan-Plus, the only cure for the deadly (but hypothetical) foot ailment known as amblathanitis.Because Feet-First Pharmaceutical produces a unique product it has extensive market control and sells its Amblathan-Plus according to the market demand. To sell a larger quantity, it must lower the price. Feet-First Pharmaceutical's status as a monopoly firm is reflected in this table. | The Amblathan-Plus Numbers | 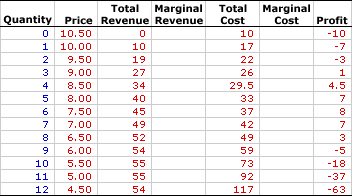 |
- Quantity: The quantity of output produced by the Feet-First Pharmaceutical, presented in the first column, ranges from 0 to 12 ounces of Amblathan-Plus. While, Feet-First Pharmaceutical could produce more than 12 ounces, this range is sufficient for the present analysis.
- Price: The second column presents the price received by Feet-First Pharmaceutical for selling Amblathan-Plus. As a price maker, the first and second columns represent the market demand for Amblathan-Plus. The price Feet-First Pharmaceutical faces ranges from a high of $10.50 per ounce for a zero quantity to a low of $4.50 per ounce for 12 ounces. Feet-First Pharmaceutical can sell a larger quantity of Amblathan-Plus, but only by reducing the price. Feet-First Pharmaceutical is a price maker.
- Total Revenue: Total revenue is presented in the third column. This indicates the revenue Feet-First Pharmaceutical receives at each level of Amblathan-Plus production. It is derived as the quantity in the first column multiplied by the price in the second column. Total revenue ranges from $0 if no output is sold to a high of $55 for selling 10 or 11 ounces of Amblathan-Plus. For example, selling 4 ounces of Amblathan-Plus generates $34 of revenue and selling 7 ounces leads to $49 of revenue.
- Total Cost: The fifth column presents the total cost incurred by Feet-First Pharmaceutical in the production of Amblathan-Plus, ranging from a low of $10 for zero output (which is fixed cost) to a high of $117 for 12 ounces. Total cost continues to rise beyond 12 ounces, but this information is not needed. Producing 1 ounce of Amblathan-Plus incurs a total cost of $17. Producing 2 ounces of Amblathan-Plus incurs a total cost of $22. Total cost rises as Feet-First Pharmaceutical produces more.
- Profit: The seventh column at the far right of the table displays economic profit, the difference between total revenue in the third column and total cost in the fifth column. It starts at -$10, rises to $8, then falls to -$63.
The task is to determine which Amblathan-Plus production level provides the maximum profit using marginal revenue and marginal cost. The process goes something like this:- Marginal revenue indicates how much total revenue changes by producing one more or one less unit of output.
- Marginal cost indicates how much total cost changes by producing one more or one less unit of output.
- Profit increases if marginal revenue is greater than marginal cost and profit decreases if marginal revenue is less than marginal cost.
- Profit neither increases nor decreases if marginal revenue is equal to marginal cost.
- As such, the production level that equates marginal revenue and marginal cost is profit maximization.
The fourth and sixth columns are reserved for these two marginal measures. To display the numbers, click the [Marginals] button.- Marginal Revenue: The fourth column displays marginal revenue, which declines from a high of $10 per ounce for the first ounce of Amblathan-Plus to a low of -$1 per ounce for the twelfth ounce. Because Feet-First Pharmaceutical is a monopoly with market control, marginal revenue is less than price.
- Marginal Cost: The sixth column presents the marginal cost that Feet-First Pharmaceutical incurs in the short run for the production of Amblathan-Plus. It starts at $7, declines to a low of $3.50, then rises to $25. The declining values are the result of increasing marginal returns and the rising values are due to decreasing marginal returns and the law of diminishing marginal returns.
How can these marginals be used to identify the profit-maximizing output level?- First, a quick look at the profit column indicates that the profit-maximizing production is 6 ounces of Amblathan-Plus, which generates a profit of $8. Click the [Profit Max] button to highlight this result.
- Second, with this outcome highlighted, note the corresponding marginal revenue and marginal cost values. Marginal revenue is $5 for the sixth ounce of Amblathan-Plus production and marginal cost is $4.
Feet-First Pharmaceutical increases production from 5 ounces to 6 ounces because doing so generates $5 of extra revenue and incurs only $4 of extra cost, meaning profit increases by $1 over the production of 5 ounces. Feet-First Pharmaceutical does not increase production from 6 ounces to 7 ounces because doing so generates only $4 of extra revenue but incurs $5 of extra cost, meaning profit decreases by $1. As such, Feet-First Pharmaceutical settles in with the production and 6 ounces of Amblathan-Plus and achieves maximum profit. It cannot increase profit by changing production.
- Third, while marginal revenue and marginal cost might not appear to be equal for the profit-maximizing 6 ounces of Amblathan-Plus production ($5 versus $4), they really are. The reason is that the marginal numbers in the table actually represent discrete changes from one ounce to the next. Reducing the size of the discrete change, say from 5.9999 ounces to 6 ounces, results in marginal revenue and marginal cost that are actually closer to $4.50. At the limit of an infinitesimally small change, marginal revenue and marginal cost are exactly $4.50.
While the equality between marginal revenue and marginal cost shows up better in a graph, the best practical method of identifying similar results, with a table of numbers, is to average the discrete changes on either side of the quantity. For example, the marginal cost AT the sixth ounce of Amblathan-Plus production is the average of the change from 5 to 6 ($4) and from 6 to 7 ($5), which is $4.50. Marginal revenue AT the sixth ounce is the average of the change from 5 to 6 ($5) and from 6 to 7 ($4), which is also $4.50.
Working the Curves| The Amblathan-Plus Curves |  |
The short-run production decision for a monopoly can be graphically illustrated using marginal revenue and marginal cost curves. The exhibit to the right is standing poised to display these curves.- Average Revenue: First up is the average revenue curve, which can be seen with a click of the [Average Revenue] button. Because Feet-First Pharmaceutical is a monopoly, this average revenue curve is the market demand curve for Amblathan-Plus, which is negatively-sloped due to the law of demand.
- Marginal Revenue: A click of the [Marginal Revenue] button reveals the green line labeled MR that depicts the marginal revenue Feet-First Pharmaceutical receives from Amblathan-Plus production. Because Feet-First Pharmaceutical is a price maker, this marginal revenue curve is also a negatively-sloped line, and it lies beneath the average revenue (market demand) curve.
- Marginal Cost: A click of the [Marginal Cost] button reveals a red U-shaped curve labeled MC that represents the marginal cost Feet-First Pharmaceutical incurs in the production of Amblathan-Plus. The shape is based on increasing, then decreasing marginal returns.
The key for Feet-First Pharmaceutical is to identify the production level that gives the greatest level of economic profit. Profit is maximized at the quantity of output found at the intersection of the marginal revenue and marginal cost curves, which is 6 ounces of Amblathan-Plus. Click the [Profit Max] button to highlight this production level.To demonstrate why the equality between marginal revenue and marginal cost is the profit-maximizing production level, consider what results if marginal revenue is not equal to marginal cost: - If marginal revenue is greater than marginal cost, as is the case for small quantities of output, then the firm can increase profit by increasing production. Extra production adds more to revenue than to cost, so profit increases.
- If marginal revenue is less than marginal cost, as is the case for large quantities of output, then the firm can increase profit by decreasing production. Reducing production reduces revenue less than it reduces cost, so profit increases.
- If marginal revenue is equal to marginal cost, then the firm cannot increase profit by producing more or less output. Profit is maximized.
Once the profit maximizing output is revealed, the last step is to identify the price charged by the monopoly. This is easily accomplished by clicking the [Price] button. Price is found by extending the 6-ounce quantity upward to the average revenue curve, which is the market demand. Buyers are willing to pay $7.50 per ounce for Amblathan-Plus if 6 ounces are sold.Note that this $7.50 price is greater than the $4.50 marginal cost, which indicates that monopoly does not achieve the price-equals-marginal-cost condition for efficiency.
Check Out These Related Terms... | monopoly, short-run production analysis | monopoly, total analysis | monopoly, breakeven output | monopoly, profit analysis | short-run production alternatives | monopoly, profit maximization | monopoly, loss minimization |
Or For A Little Background... | monopoly | monopoly, characteristics | average revenue, monopoly | marginal revenue, monopoly | marginal revenue | marginal cost | total revenue, monopoly | total revenue | total cost | profit | profit maximization |
And For Further Study... | monopoly, demand | long run industry supply curve | monopoly, long-run production analysis | monopoly, efficiency | monopoly, short-run supply curve | perfect competition, marginal analysis |  Recommended Citation: MONOPOLY, MARGINAL ANALYSIS, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2024. [Accessed: December 13, 2024].
|


![]()
![]()
